线性规划

例题 1

$z = 10x + 10y, \max{z} = $ ？

基本概念

1. 约束条件：变量 $x,y,\dots$ 满足的一组条件，上述二元一次不等式组就是对 $x,y$ 的约束条件。
2. 线性约束条件：由变量 $x,y,\dots$ 的一次不等式 / 方程组成的不等式组就称为线性约束条件，如上述二元一次不等式。
3. 目标函数：欲求最大值或最小值所涉及的变量 $x,y,\dots$ 的解析式，如上述 $z$.
4. 线性目标函数：目标函数关于变量 $x,y,\dots$ 的一次解析式，如上述 $z$.
5. 线性规划问题：在线性约束条件下求线性目标函数的问题。
6. 可行解：满足线性约束条件的解 $(x,y)$.
7. 可行域：由所有可行解组成的集合。
8. 最优解：使目标函数取得 $\max$ 或 $\min$ 的可行解。

解法

1. 画图，数形结合。

$$\begin{cases}5x-11y \geq -22 & \displaystyle \implies y \leq \frac{5}{11}x + \frac{1}{2} & \implies & \displaystyle y = \frac{5}{11}x + \frac{1}{2}\ 图像的下边 \\ 2x+3y \geq 9 & \displaystyle \implies y \geq -\frac{2}{3}x + 3 & \implies & \displaystyle y = -\frac{2}{3}x + 3\ 图像的上边 \\ 2x \leq 11 & \displaystyle \implies x \leq \frac{11}{2} & \implies & \displaystyle x=\frac{11}{2}\ 图像的左边 \end{cases}$$

在平面直角坐标系上画出对应的平面区域（可行域），再把目标函数 $z=ax+by$ 变形为 $\displaystyle y=-\frac{a}{b}x + \frac{z}{b}$，$\\$ 所以求 $z$ 的最值可看成是求直线 $\displaystyle y=-\frac{a}{b}x + \frac{z}{b}$ 在 $y$ 轴上截距的最值。以这题为例，$\displaystyle z=10x+10y \implies y= -x + \frac{z}{10}$ 容易证明，当 $z=85$ 时 $y$ 轴上截距取最值，所以 $\max{z}=85.$

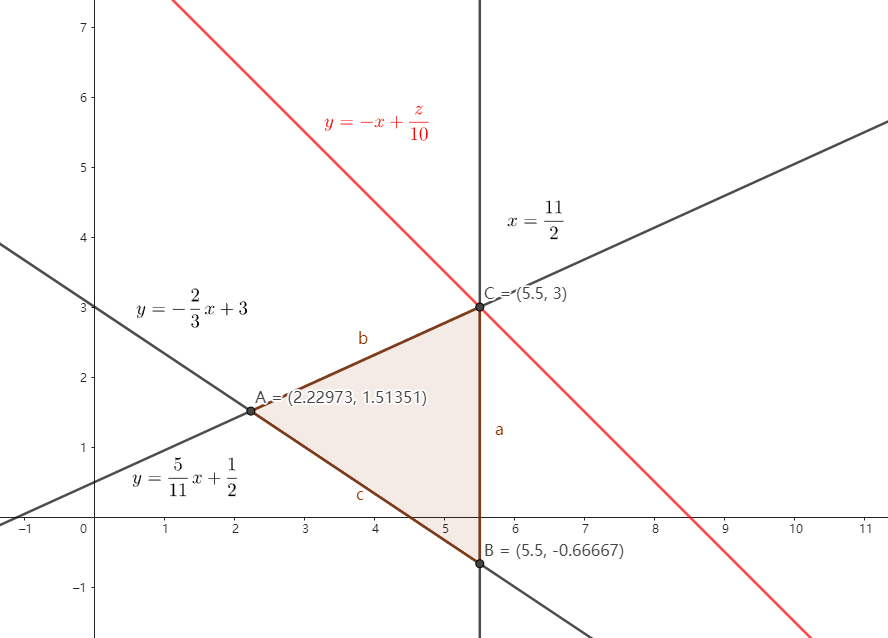
1. 仔细观察，可以发现最优解非常容易出现在可行域构成的多面体的顶点处。

例题 2

$(2x+y){\mathrm{max}}=4(2x+y), a= $ ?}

• 求 $(2x+y)_{\mathrm{min}}$：$x_{\min}=a \implies y_{\min}=a \implies (2x+y)_{\mathrm{min}}=3a$

• 求 $(2x+y)_{\mathrm{max}}$：$\begin{cases}x-y\leq 0 \\ x+y\leq 2\end{cases}\xRightarrow{\mathrm{Add\ }} x\leq 1\implies y\leq 1\implies (2x+y)_{\mathrm{max}}=3$

• $\displaystyle 3=4\times 3a\implies a=\frac{1}{4}$

例题 3（2024 九省联考 T14）

$\max{\set{b-a,c-b,1-c}}$ 的最小值 $=$ ？

• 注意到 $c$ 的约束条件是最少的，首先考虑消去它，得到

$\ \ \ \ \ \ \text{}$ 当且仅当 $\displaystyle c=\frac{1+b}{2}$ 取等，消去 $c$ 后把 $a$ 看作 $x$，把 $b$ 看作 $y$ 得：

• 作出可行域：$\mathrm{and}$ 连接的区域之间取交，$\mathrm{or}$ 连接的区域之间取并。阴影部分即为可行域。

$\ \ \ \ \ \ \text{}$ 图中 $y\geq 2x\ \ \ x+y\leq 1$ 两条解析式用红色标出。

• 回到题目，要求 $\displaystyle M=\max{\set{y-x,\frac{1-y}{2}}}$，我们需要知道何时 $M=y-x$，何时 $\displaystyle M=\frac{1-y}{2}$.

$\ \ \ \ \ \ \text{}$ 直接列方程 $\displaystyle y-x=\frac{1-y}{2}$ 可以得到 $\displaystyle y=\frac{2}{3}x+\frac{1}{3}$，在图中作出这条直线，得到：

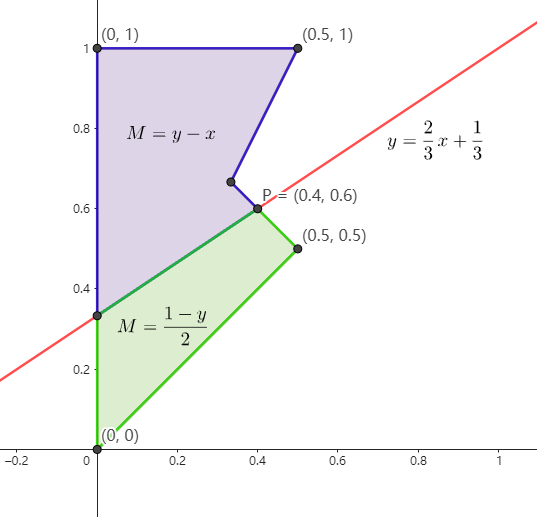
• 因为最终要求的是 $M$ 的最小值，所以对蓝色区域而言，$y$ 尽量小，$x$ 尽量大，根据例题 1 的经验，这样的极值点通常出现在多边形的顶点处，经过比较后 $P$ 点是极值点，此时 $M=0.2$. 对绿色区域而言，只需满足 $y$ 尽量大，显然，$P$ 点也是极值点。
• 综上所述，$\max{\set{b-a,c-b,1-c}}$ 的最小值 $\displaystyle=\frac{1}{5}$.

https://oi-wiki.org/math/linear-programming/#%E5%BC%95%E5%85%A5